Inverse functions are mathematical operations where the output of one function becomes the input of another, reversing the original function’s operation. The inverse function, denoted as f⁻¹(x), undoes the action of f(x), making them essential in solving equations and understanding relationships. They are widely used in algebra, calculus, and real-world applications like engineering and economics. Mastering inverse functions enhances problem-solving skills and deepens mathematical understanding.
1.1 Definition of Inverse Functions
An inverse function reverses the action of another function. For a function ( f(x) ), its inverse, denoted as ( f^{-1}(x) ), satisfies the property ( f(f^{-1}(x)) = x ) and ( f^{-1}(f(x)) = x ). This means that if ( f ) maps ( x ) to ( y ), then ( f^{-1} ) maps ( y ) back to ( x ). The process involves swapping variables and solving for ( y ), ensuring the original function is bijective (one-to-one and onto). Understanding this concept is fundamental for solving equations and real-world problems effectively.
1.2 Importance of Inverse Functions in Mathematics
Inverse functions are crucial in mathematics as they enable the reversal of operations, solving equations, and simplifying complex problems. They are essential in calculus for understanding integrals and derivatives. Inverse functions also play a key role in cryptography, engineering, and economics. Mastery of inverses enhances algebraic manipulation skills and deepens the understanding of function behavior. Worksheets with answers, like the inverse function worksheet with answers PDF, provide structured practice, helping students grasp this fundamental concept and its wide-ranging applications.
How to Find the Inverse of a Function
To find the inverse of a function, switch the roles of x and y, then solve for y. This step-by-step process ensures the inverse is correctly determined.
2.1 Steps to Find the Inverse
To find the inverse of a function, start by replacing f(x) with y. Then, interchange x and y to reflect the inverse relationship. Next, solve for y to express the inverse function. Finally, verify the inverse by ensuring that f(f⁻¹(x)) = x and f⁻¹(f(x)) = x. This step-by-step process guarantees accuracy and confirms the inverse function’s validity.
2.2 Examples of Finding Inverses
For example, to find the inverse of f(x) = 2x + 1, swap x and y to get x = 2y + 1, then solve for y: y = (x ⸺ 1)/2. Thus, the inverse is f⁻¹(x) = (x ⸺ 1)/2. Another example: for f(x) = x² ⸺ 3x, swap variables to get x = y² ‒ 3y, rearrange to y² ‒ 3y ⸺ x = 0, and solve for y using the quadratic formula. These examples illustrate the systematic approach to finding inverses.
An inverse function worksheet with answers PDF provides a structured approach to practicing the concept of inverse functions. It includes a variety of exercises, detailed solutions, and answers, allowing students to test their understanding and improve their skills in finding inverses. The worksheet is an essential resource for mastering inverse functions.
The inverse function worksheet with answers PDF is divided into sections, each focusing on specific skills. It begins with warm-up exercises to recall definitions and moves to advanced problems. The structure includes multiple-choice questions, fill-in-the-blanks, and open-response tasks. Each problem set is followed by detailed solutions, allowing students to verify their work. The worksheet also includes graphing activities to visualize inverse relationships, enhancing understanding; This organized format ensures comprehensive practice and mastery of inverse functions. The worksheet includes a variety of problems to cater to different learning needs. It features questions on finding inverse functions, verifying inverses, and graphing inverse relationships. Students practice solving equations, composing functions, and determining domain restrictions. Multiple-choice questions, fill-in-the-blanks, and open-response tasks are included for comprehensive understanding. Additionally, problems involve restricted domains and one-to-one functions, ensuring a thorough grasp of inverse function concepts. The exercises are designed to enhance analytical and problem-solving skills, making the worksheet a versatile learning tool. The inverse function worksheet offers numerous benefits for students. It provides hands-on practice, reinforcing the understanding of inverse functions through varied exercises. The included answers enable immediate feedback, helping students identify and correct mistakes. The structured format supports independent study, allowing learners to work at their own pace. By solving diverse problems, students enhance their problem-solving skills and mathematical reasoning. Additionally, mastering inverse functions through this worksheet prepares learners for more advanced topics in algebra and calculus. Regular practice builds confidence and fluency in manipulating functions. The worksheet covers one-to-one functions, domain restrictions, and graphing inverses. It includes finding inverses, verifying solutions, and understanding function relationships. Real-world applications are also explored. One-to-one functions are essential for finding inverses, as they ensure each input maps to a unique output and vice versa. The worksheet emphasizes identifying such functions, using methods like the horizontal line test. It also covers restricting domains to make functions one-to-one, a key step in finding inverses. By mastering this concept, students can determine which functions have inverses and understand the relationship between functions and their inverses, enhancing their algebraic and graphical analysis skills. Domain and range restrictions are crucial for ensuring functions are one-to-one, allowing them to have inverses. The worksheet includes exercises where students restrict domains and ranges to make functions invertible. For example, restricting the domain of a quadratic function makes it one-to-one, enabling an inverse. This concept is vital for understanding how functions and their inverses relate graphically and algebraically, helping students grasp the principles of invertibility and apply them to various mathematical problems. Graphing inverse functions helps visualize their relationship, as they are reflections of each other across the line y = x. The worksheet includes exercises where students plot original functions and their inverses on the same coordinate plane. By identifying corresponding points and drawing reflections, learners gain a deeper understanding of how inverses operate. This practical approach reinforces the concept of function-inverse pairs and their symmetrical properties, making abstract ideas more tangible and easier to grasp. The worksheet includes a variety of practice problems, such as finding inverses of linear and nonlinear functions, with step-by-step solutions provided for clarity and understanding. Solving for inverses involves reversing the mapping of a function to find its corresponding inverse. Start by replacing f(x) with y, then interchange x and y, and finally solve for y. For example, given f(x) = 2x + 3, set y = 2x + 3, swap to x = 2y + 3, and solve for y to get y = (x ⸺ 3)/2. The worksheet provides step-by-step examples and solutions, helping students master the process. Practice problems cover linear and nonlinear functions, ensuring a thorough understanding of inverse operations. Verifying inverses ensures that two functions are true inverses of each other. To confirm, compose the functions: f(g(x)) and g(f(x)) should both equal x. For example, if f(x) = 2x + 3 and g(x) = (x ‒ 3)/2, then f(g(x)) = 2((x ‒ 3)/2) + 3 = x, and g(f(x)) = (2x + 3 ⸺ 3)/2 = x. The worksheet provides exercises to practice this verification process, reinforcing the concept and ensuring accuracy in determining inverse functions. This step is crucial for confirming the correctness of the inverse. Common mistakes include misapplying inverse operations, forgetting to restrict domains, and improper switching of variables. Carefully follow steps to ensure accurate inverses. Avoid algebraic errors.
A prevalent mistake is misunderstanding that an inverse function undoes the original function’s operation. Students often confuse inverses with reciprocal functions or negative exponents. It’s crucial to recognize that f⁻¹(x) is not merely -f(x) but a function that satisfies f(f⁻¹(x)) = x. Additionally, assuming all functions have inverses is incorrect; only one-to-one functions qualify. Misconceptions can hinder problem-solving and application of inverse functions in various mathematical contexts. Clear understanding is essential for accurate computations and graphing. Algebraic errors often occur when finding inverse functions, particularly during the process of interchanging variables and solving for y. Common mistakes include incorrectly switching x and y, mishandling coefficients, and improperly rearranging equations. For example, students may forget to apply inverse operations correctly or mismanage fractions and negative signs. Such errors can lead to incorrect inverses and failed verifications. To avoid these, students should carefully follow each step, double-check their algebra, and verify their solutions by composing the function and its inverse to ensure they yield the identity function. This section provides detailed solutions and final answers to inverse function problems, ensuring accuracy and helping students master the concept and identify common errors. This section provides step-by-step explanations for finding inverse functions, ensuring students understand the process. Each problem is solved methodically, starting with swapping variables, solving for y, and verifying the inverse. Examples include functions like f(x) = 2x + 1, where the inverse is found by interchanging x and y, resulting in f⁻¹(x) = (x ⸺ 1)/2. Detailed solutions help students identify common mistakes and grasp the concept thoroughly. Practice problems and their solutions are included to reinforce learning and mastery of inverse functions. The final answers section offers a quick reference for students to verify their solutions. Each problem’s correct inverse function is provided, ensuring accuracy. For example, if the function is f(x) = 3x ‒ 2, the final answer is f⁻¹(x) = (x + 2)/3. These concise answers help students assess their understanding and identify areas needing review. The section is designed to promote self-checking and confidence in solving inverse function problems. The worksheet provides links to online tools, supplementary worksheets, and educational websites like Khan Academy and Mathway for further practice and understanding of inverse functions. Websites like Khan Academy and Mathway offer interactive tools to practice finding inverse functions. Kuta Software provides worksheets with answers for self-assessment. These platforms allow students to explore inverse functions through guided examples, video tutorials, and customizable practice problems. They also include graphing capabilities to visualize functions and their inverses, enhancing understanding. Additionally, forums and discussion groups provide support for troubleshooting common mistakes. These resources make learning inverse functions engaging and accessible for all skill levels; Supplementary worksheets are excellent resources for additional practice with inverse functions. They often include a variety of problems, from basic to advanced, covering one-to-one functions, domain restrictions, and graphing inverses. Many worksheets, such as those from Kuta Software and Maths4Everyone, provide detailed solutions, enabling self-assessment and verification of answers. These materials are ideal for reinforcing concepts learned in class or through self-study, offering a structured approach to mastering inverse functions. They also help identify common mistakes and improve problem-solving skills.3.1 Structure of the Worksheet
3.2 Types of Problems Included
3.3 Benefits of Using the Worksheet
Topics Covered in the Worksheet
4.1 One-to-One Functions
4.2 Domain and Range Restrictions
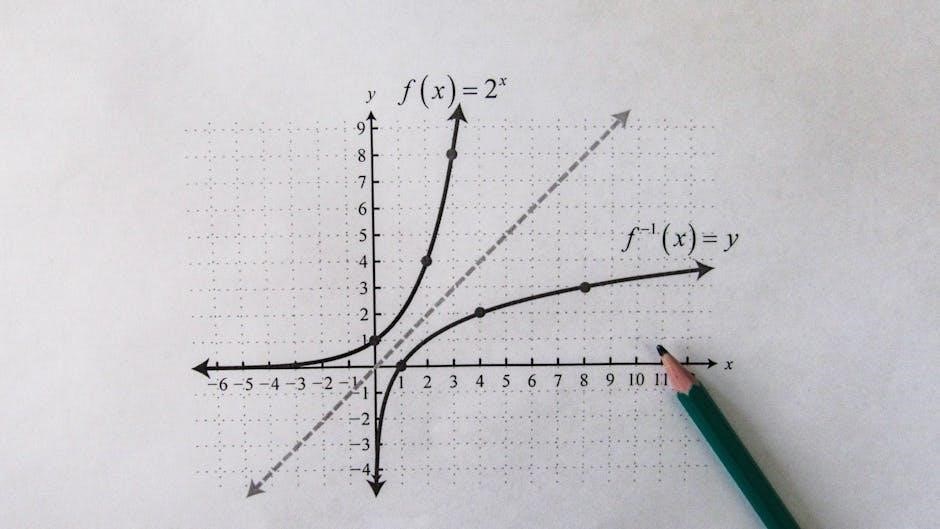
4.3 Graphing Inverse Functions

Practice Problems and Solutions
5.1 Solving for Inverses
5.2 Verifying Inverses

Common Mistakes to Avoid
6.1 Misunderstanding the Concept of Inverses
6.2 Algebraic Errors During the Process
Answers and Solutions
7.1 Detailed Solutions
7.2 Final Answers

Additional Resources
8.1 Online Tools for Practice
8.2 Supplementary Worksheets
Understanding inverse functions is a fundamental skill in mathematics, essential for solving equations and grasping relationships between variables. The inverse function worksheet with answers pdf serves as a valuable tool for mastering this concept, offering practice problems and detailed solutions. By working through these exercises, students can improve their algebraic manipulation skills and deepen their understanding of function behavior. Regular practice and review of inverse functions will enhance problem-solving abilities and prepare learners for advanced mathematical studies.
